Прошедшая в рамках образовательного интенсива «PROНаука в КФУ» лекция доктора физико-математических наук, заведующего кафедрой геометрии Института математики и механики им. Н.И. Лобачевского Аркадия Попова называлась «О началах геометрии и ее современных достижениях».

Во время нее ученый рассказал об истории развития геометрии и о том, как она используется в современной науке.

Первая попытка перечислить определения и аксиомы, на основе которых можно развивать науку строго логическим путем, была сделана в III веке до нашей эры Евклидом в его главном труде «Начала», сообщил математик.

«Идея тринадцати книг Евклида (сейчас бы мы их назвали главами) состояла в следующем: он выдвинул утверждения, в которые все верили, в качестве аксиом. У Евклида они назывались аксиомами и постулатами. Основная идея состояла в следующем: утверждения, выбираемые в качестве аксиом, не доказываются, а все остальные – извлекаются из них в процессе логических рассуждений. Это породило первую науку – геометрию», – объяснил Аркадий Александрович.

Конечно, аксиоматика Евклида была несовершенной, отметил математик. Часть аксиом в дальнейшем удалось доказать исходя из остальных. Но в современной науке есть аксиомы, которые в «Началах» Евклида отсутствовали.

«Последний, пятый из постулатов Евклида, был введен им не сразу, и часть теорем в первых книгах на него не опиралась. Этот постулат является громоздким и среди других достаточно очевидных постулатов выглядит чужеродным. В современных школьных учебниках он был заменен эквивалентным утверждением: аксиомой параллельности», – проинформировал спикер и добавил, что Лобачевский был одним из первых, кто понял, что доказать V постулат невозможно.

Аксиома параллельности (пятый постулат Евклида) гласит, что через любую точку плоскости, расположенную вне данной прямой, можно провести не более одной прямой, не пересекающей данную прямую. Аксиома Лобачевского, которая является отрицанием аксиомы параллельности, утверждает обратное: через любую точку плоскости, расположенную вне данной прямой, можно провести более одной прямой, не пересекающей данную. Решение проблемы: если пятый постулат не следует из других аксиом геометрии, то и его отрицание не может противоречить другим аксиомам, и, следовательно, существует еще одна геометрия.

Сравнивая геометрию Евклида и Лобачевского, А. Попов отметил, что неевклидова геометрия Лобачевского дала импульс развитию науки.

«Для того чтобы понять геометрию Лобачевского, надо понять, что такое прямая. Она, как известно, позволяет определить кратчайшее расстояние между двумя точками. Но если идет речь, например, о сфере, то кратчайшим расстоянием между двумя точками будет дуга большой окружности. Такие линии стали называть геодезическими. Они и являются аналогами прямых на плоскости», – сказал доктор наук.  

На сфере любые геодезические линии будут пересекаться, сообщил он.

«Через точку вне геодезической на сфере нельзя провести другую геодезическую, которая данную геодезическую не пересекает. В дальнейшем такие рассуждения позволили понять, что геометрия Лобачевского – это геометрия псевдосферы», – разъяснил А. Попов.

Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера.

«Если с точками и прямыми сопоставлять точки и линии, определяющие кратчайшие расстояния между точками (геодезические), на псевдосфере, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере», – подчеркнул выступающий.

Далее ученый КФУ рассказал о том, что Б. Риман обобщил геометрию Лобачевского на случай произвольной поверхности (и не только поверхности), а А. Эйнштейн воспользовался римановой геометрией для создания общей теории относительности.

«Гравитационное взаимодействие в теории Альберта Эйнштейна является следствием искривления четырехмерного пространства-времени», – в частности сказал геометр.

По словам ученого КФУ, уравнения общей теории относительности Эйнштейна были написаны в конце 1915 года, а в 1916 году ученый-астроном Карл Шварцшильд, основываясь на них, дал описание экзотических объектов Вселенной, черных дыр, о существовании которых никто тогда не подозревал.

«Для того чтобы создать черную дыру с массой Земли, необходимо всю эту массу сжать до размеров шара величиной с горошину. Ученые считают, что в центре нашей галактики находится гигантская черная дыра, вокруг которой вращаются звезды», – заметил он.

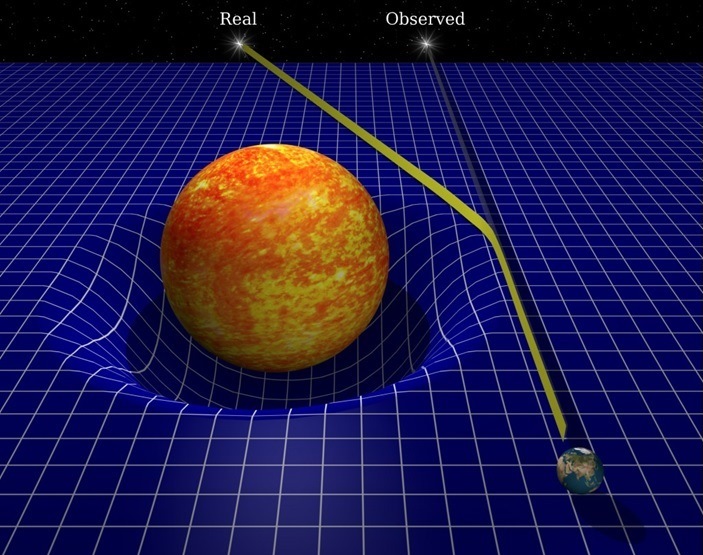
«Теория относительности Эйнштейна была построена в конце 1915 – начале 1916 года, а ее первое подтверждение было сделано в 1919 году. Ученые обнаружили отклонение луча света, идущего от звезды, в гравитационном поле Солнца. Это было явное подтверждение теории Эйнштейна», – поделился знаниями геометр.

Еще одним крупным научным достижением, связанным с теорией относительности, стало создание теории эволюции Вселенной.

«Первый результат в этом направлении получил Александр Фридман в 1921 году. Он получил решения уравнений теории гравитации Эйнштейна, описывающие расширяющуюся Вселенную. Сам Эйнштейн изначально считал, что Вселенная статична. Однако эффект расширения Вселенной был обнаружен в 1929 году Хабблом», – сказал А. Попов, отметив, что современные наблюдения обнаружили ускоренное расширение Вселенной.

Это, в свою  очередь, означает, что мы не понимаем, что представляет собой большая часть материи (темная энергия) Вселенной. Описание этого ускоренного расширения является одним из направлений исследований современной геометрии и теории гравитации.

С подробной программой мероприятия и записями лекций можно ознакомиться на сайте «PROНаука в КФУ».